반응형
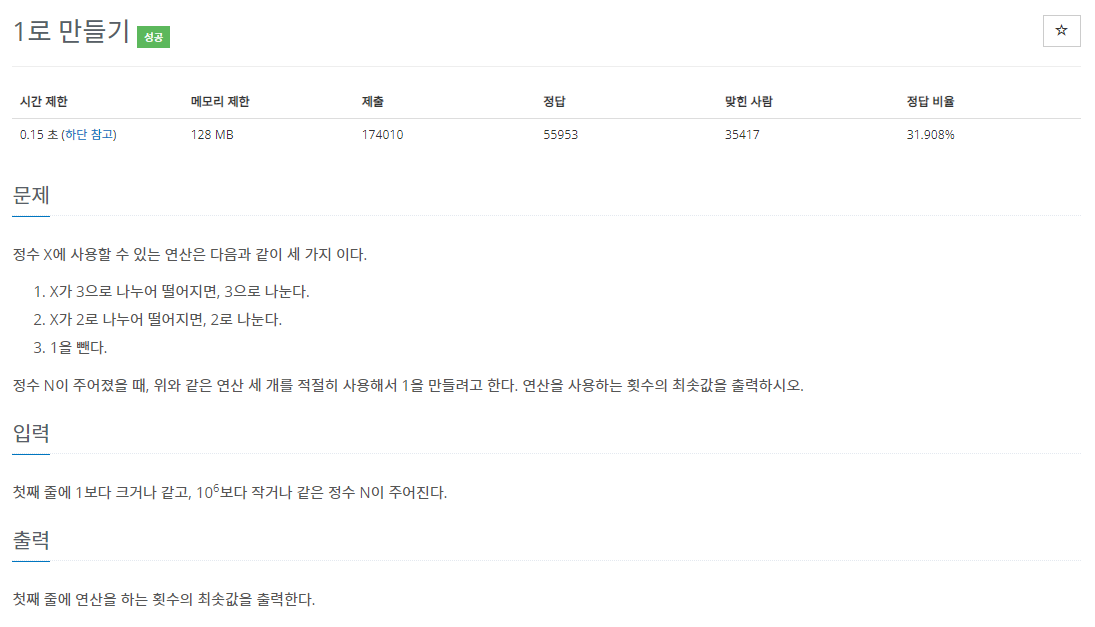
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
📌 다이나믹 프로그래밍
[Algorithm] 다이나믹 프로그래밍 | Dynamic Programming | 계속 쓰일 값은 저장해놓고 가져다 쓰자
💡 다이나믹 프로그래밍 (Dynamic Programming, DP) 우리는 연산 속도와 메모리 공간을 최대한 활용할 수 있는 효율적인 알고리즘을 작성해야 한다. 그런데 어떤 문제는 메모리 공간을 약간만 더 사용
eunbin00.tistory.com
1이 될 때까지 주어진 연산을 최소로 사용하는 '1로 만들기' 문제는 다이나믹 프로그래밍 알고리즘을 활용하는 대표적인 유형이다.
이 문제가 다이나믹 프로그래밍 알고리즘을 사용하여 풀 수 있는 조건은 다음과 같다.
- 주어지는 수 X를 1로 만들기 위한 최소 연산 횟수는 항상 같다.
- X를 1로 만들기 위한 최소 연산 횟수를 구하기 위해서 X에 각 연산을 적용했을 때의 최소연산 횟수의 결과값이 필요하며 이는 또다시 반복된다.
즉, X의 최소연산횟수를 구하는 함수를F(X)라고 가정하면, F(X)를 구하기 위해서는 F(X_연산1적용), F(X_연산2적용)... 이 필요하고, F(X_연산1적용)을 구하기 위해서는 F(X_연산1적용_연산1적용), F(X_연산1적용_연산2적용)... 의 값들이 필요하다.
✅ 문제 풀이 소스 코드
x = int(input())
d = [0] * (x+1)
for i in range(2, x+1):
d[i] = d[i-1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i//2]+1)
if i % 3 == 0:
d[i] = min(d[i], d[i//3]+1)
print(d[x])- 각 X에 대한 최소 연산 값을 저장하기 위한 리스트
d를 생성한다. - 문제 해결 아이디어는 점화식으로 표현하면 $$a_i = min(a_{i_1}, a_{i/2}, a_{i/3})+1$$이다.
예를 들어, 12의 최소 연산 횟수는 11(=12-1)의 연산횟수(=d[11]), 6(=12/2)의 최소 연산 횟수(=d[6]), 4(=12/3)의 최소 연산 횟수(=d[4]) 중 최솟값 + 1이다. - 2의 최소 연산 횟수부터 X의 최소 연산 횟수까지 계산함으로써 차례대로 DP 테이블에 저장된 값을 이용한다. → Bottom-Up 방법
반응형
'Algorithm > BOJ' 카테고리의 다른 글
| BAEKJOON #11718) 그대로 출력하기| C, Python (0) | 2022.02.15 |
|---|---|
| BAEKJOON #9663) N-QUEEN (C) (0) | 2022.01.31 |
| BAEKJOON #12865) 평범한 배낭🎒 | knapsack | dynamic programming (0) | 2021.12.09 |
| BAEKJOON #1026) 보물 (0) | 2021.10.11 |
| BAEKJOON #2231) 분해합 (python) (0) | 2021.10.10 |




댓글