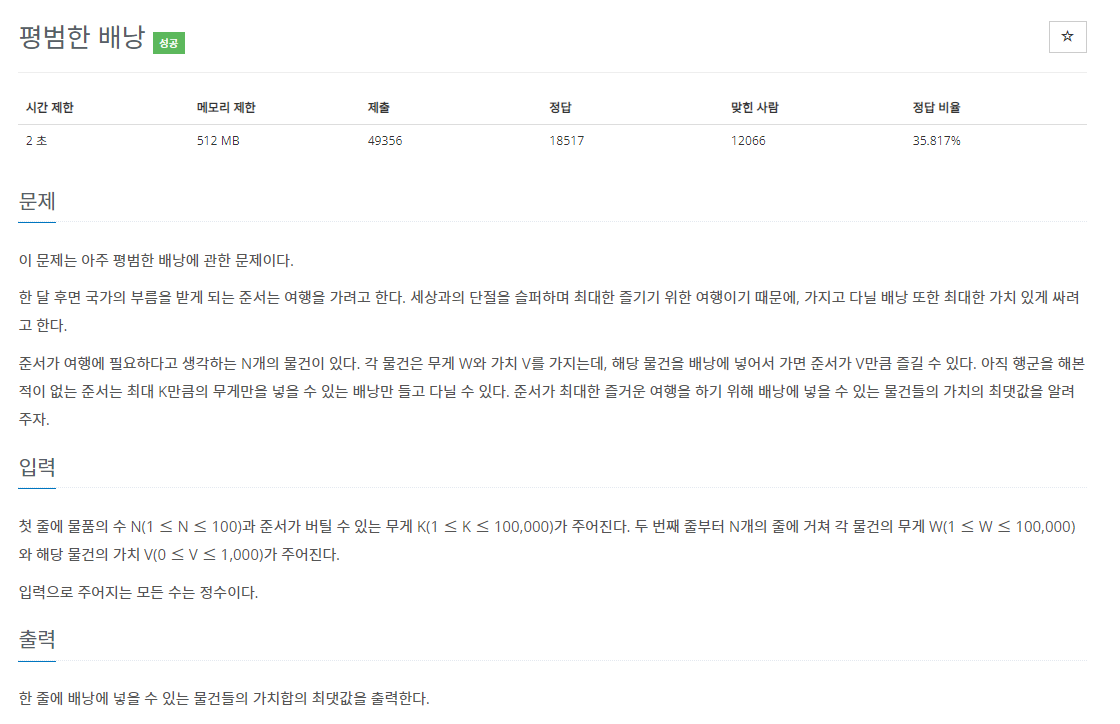
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
🎒
백준 12865번 평범한 배낭 문제는 다이나믹 프로그래밍의 대표적인 문제 유형인 knapsack(배낭) 문제이다.
[Algorithm] 다이나믹 프로그래밍 | Dynamic Programming | 계속 쓰일 값은 저장해놓고 가져다 쓰자
💡 다이나믹 프로그래밍 (Dynamic Programming, DP) 우리는 연산 속도와 메모리 공간을 최대한 활용할 수 있는 효율적인 알고리즘을 작성해야 한다. 그런데 어떤 문제는 메모리 공간을 약간만 더 사용
eunbin00.tistory.com
knapsack 문제는 배낭에 담을 수 있는 최대 무게와 물건들의 무게와 가치가 주어질 때, 배낭에 담을 수 있는 최대 가치를 계산하는 문제이다.
이때 물건을 쪼갤 수 없으면 0-1 knapsack problem, 쪼갤 수 있으면 fractional knapsack problem으로 부른다. 12865번 문제는 물건을 쪼갤 수 없으므로 0-1 knapsack 문제이다.
🎒 knapsack과 Dynamic Programming
knapsack problem에 적용되는 알고리즘은 최대 허용 무게가 1일 때부터 계산하여 그 결과값을 리스트에 저장하고, 더 큰 최대 허용 무게를 계산할 때 앞서 저장된 값들을 사용해서 문제를 푸는 Dynamic Programming 알고리즘이다.
🎒 knapsack 풀이 (적용 수식)
2차원 리스트에서 각각의 element들을 채울 때 적용되는 수식은 다음과 같다.
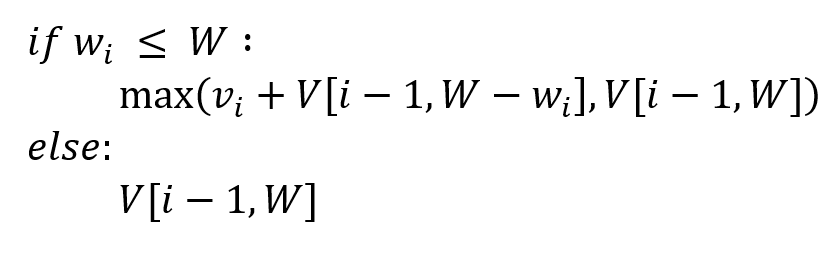
w_i와 v_i는 각각 현재 돌고 있는 물건의 무게와 가치의 값이고, W는 현재 돌고 있는 최대 허용 무게이다. V는 각 인덱스에서의 가치를 계산한 값(각 셀에 들어가 있는 값)이다.
우선, 현재 돌고 있는 물건의 무게가 최대 허용 무게보다 큰지 아닌지 확인한다. (즉, 현재 돌고 있는 물건을 현재 배낭에 넣을 수 있는지 없는지 검사한다.)
- 현재 물건을 배낭에 넣을 수 있다면 (조건절이 참이라면)
2가지의 선택권이 생긴다. 현재 물건을 넣을 건지, 넣지 않을건지! 그렇다면 현재 물건을 넣었을 때 가치가 더 큰지, 넣지 않았을 때 가치가 더 큰지 체크해야한다.
즉, 현재 물건을 넣고 그 나머지 공간에 넣을 수 있는 물건을 넣었을 때의 가치가 더 큰지, 아니면 현재 물건을 넣지 않고 그 이전 물건들로만 계산되는 가치가 더 큰지 확인하여 더 큰 값을 저장한다.
- 현재 물건을 배낭에 넣을 수 없다면 (조건절이 거짓이라면):
현재 물건을 넣지 못하기 때문에 선택권이 없다. 현재 물건은 버리고 그 이전까지의 물건으로만 계산했을 때의 가치를 그대로 저장한다.
🎒 2차원 리스트의 생성
냅색 문제에서는 각각의 값을 채워넣을 때 이전 값을 활용하는 것이 필요하므로 아래처럼 최대 허용 무게가 0일때와 무게와 가치가 모두 0인 물건을 추가하여 2차원 리스트를 만들어준다. (0행과 0열을 모두 0으로 채워준다.)
n, k = map(int, input().split()) #n은 물건의 개수, k는 배낭에 넣을 수 있는 최대 무게
stuff = [[0,0]]
knapsack = [[0 for _ in range(k + 1)] for _ in range(n + 1)]
🎒 knapsack 알고리즘 따라가보기
☑️ 최대 허용 무게가 1일때
최대 가치가 1일 때부터 계산하여 그 결과값을 리스트에 저장하고, 더 큰 최대 가치를 계산할 때 앞서 저장된 값들을 활용한다. 최대 가치가 1일 때부터 물건들을 차례대로 넣어보자.
먼저 무게가 6이고 가치가 13인 물건이다. 배낭에 넣을 수 있는 최대 가치가 1인데 물건의 무게가 6이므로 넣을 수 없다. 따라서 이전 값(V[0, 1])을 가져온다.

☑️ 최대 허용 무게가 2일때
아마 최대 허용 무게가 2일 때까지는 어떤 물건도 넣지 못할 것이다. 따라서 원소값들이 모두 0이다.

☑️ 최대 허용 무게가 3일때

무게가 6과 4인 물건들은 담지 못하므로 모두 최대 가치로 모두 0이 저장되고 무게가 3인 물건을 돌 때 드디어 물건을 넣을 수 있어진다. 그럼 이제 선택해야한다. 이 물건을 넣는 것이 가치가 큰지, 넣지 않는 것이 가치가 큰지. 따질 것도 없이 물건을 넣어야 한다. 왜냐하면 지금까지의 계산된 가치의 값들은 모두 0이었기 때문에 계산할 것도 없다! 굳이 굳이 계산을 해보자면
물건을 넣었을 때의 가치는 6( = 6 + 0(나머지 공간에 넣을 수 있는 가치) )이고, 물건을 넣지 않았을 때의 가치는 0( = V[2, 3] )이다. 따라서 6을 저장해준다. 즉, 최대 허용 무게가 3일때, 3번째 물건까지만 확인했을 때, 최대 가치는 6으로 계산된 것이다.
그럼 마지막 물건까지 확인해보자. 무게가 5인 물건이다. 최대 허용 무게가 3이므로 이 물건은 넣을 수 없다. 따라서 이전 물건까지의 가치값인 6( = V[3, 3] )을 그대로 가져온다.
☑️ 최대 허용 무게가 7일 때

1. 첫번째 물건 (6, 13)
최대 허용 무게가 7인데 현재 물건의 무게가 6이다. 넣을 수 있다. 이 물건을 넣어야 가치가 클까? 이전 값을 가져오는 것이 가치가 클까? 이전값은 0이므로 당연히 이 물건은 넣어야 한다. 13을 저장한다.
2. 두번째 물건 (4, 8)
최대 허용 무게가 7인데 현재 물건의 무게가 4이다. 넣을 수 있다. 이 물건을 넣고 나머지 공간( = 2 )에 넣을 수 있는 가치( = 0 = V[1, 3] )를 더하는 것이 가치( = 8 = 8 + 0)가 큰가 아니면 첫번째 물건을 유지하는 것이 가치( = 13 )가 큰가? 첫번째 물건을 유지하여 이전 값인 13을 그대로 저장한다.
3. 세번째 물건 (3, 6)
최대 허용 무게가 7인데 현재 물건의 무게가 3이다. 넣을 수 있다. 이 물건은 넣어야 하나, 넣지 않아야 하나?
max(v_3 + V[2, 4], V[2, 7]) = max(6+8, 13) = 14이므로 현재 물건을 넣고 나머지 공간에 무게가 4인 물건을 넣어서 더 큰 가치인 14를 저장한다.
4. 네번째 물건 (5, 12)
최대 허용 무게가 7인데 현재 물건의 무게가 5이다. 넣을 수 있다. 이 물건은 넣어야 하나, 넣지 않아야 하나?
max(v_4 + V[3, 2], V[3, 7]) = max(12+0, 14) = 14이므로 무게가 5인 물건은 버리고 이전 값을 그대로 가져오는 것이 가치가 더 크므로 14를 그대로 저장한다.
☑️ BOJ #12865에서 만들어진 최종적인 2차원 리스트를 도식화하면 다음과 같다.


✅ 풀이 소스 코드
import sys
n, k = map(int, input().split())
stuff = [[0,0]]
knapsack = [[0 for _ in range(k + 1)] for _ in range(n + 1)]
for _ in range(n):
stuff.append(list(map(int, input().split())))
for i in range(1, n + 1):
for j in range(1, k + 1):
weight = stuff[i][0]
value = stuff[i][1]
if j < weight:
knapsack[i][j] = knapsack[i - 1][j]
else:
knapsack[i][j] = max(value + knapsack[i - 1][j - weight], knapsack[i - 1][j])
print(knapsack[n][k])'Algorithm > BOJ' 카테고리의 다른 글
| BAEKJOON #9663) N-QUEEN (C) (0) | 2022.01.31 |
|---|---|
| BAEKJOON #1463) 1로 만들기 | 다이나믹 프로그래밍 | python (0) | 2021.12.10 |
| BAEKJOON #1026) 보물 (0) | 2021.10.11 |
| BAEKJOON #2231) 분해합 (python) (0) | 2021.10.10 |
| BAEKJOON #1417) 국회의원 선거 (python) (0) | 2021.09.05 |




댓글