최단 경로 알고리즘은 말 그대로 가장 짧은 경로를 찾는 알고리즘입니다.
어떤 한 지점에서 다른 한 지점까지의 최단 경로를 찾아야 하는 문제의 경우, 각 지점은 그래프의 노드로, 지점 간 거리는 간선의 가중치로 표현됩니다. 즉, 아래 그림과 같은 각 간선이 가중치를 갖는 유향 그래프로 표현됩니다.

🚗 최단 경로
두 정점 사이의 최단 경로의 길이는 가중치들의 합 중에서 가장 작은 값을 가지는 경로이다. 만약 어떤 두 정점 사이의 최단 경로가 없다면 이때의 거리는 무한대($\infty$)라고 가정합니다.
그렇다면 최단 경로를 어떻게 찾을 수 있을까요? 단순하게는 모든 경로에 대한 거리를 계산해보고 가장 짧은 경로를 선택하면 됩니다. 하지만 이 방법은$n$개의 정점이 있을 때, $(n-2)!$개의 경로의 거리를 계산해야 합니다. 30개의 정점만 있어도 계산해야 하는 양이 어마어마하기 때문에 매우 오랜 시간이 걸립니다.
이를 해결할 수 있는 최단 경로 알고리즘들이 있는데, 대표적으로는 다익스트라 알고리즘, 플로이드 워셜 알고리즘, 벨만 포드 알고리즘이 있습니다. 오늘은 이중에서도 다익스트라(E.W. Dijkstra) 알고리즘에 대해서 공부해보겠습니다.
다익스트라 알고리즘은 출발 정점으로부터 모든 정점들의 최단경로를 계산할 수 있습니다.
다익스트라 알고리즘은 최단 경로를 구하는 과정에서 각 노드에 대한 현재까지의 최단 거리 정보를 항상 1차원 리스트에 저장하며 리스트를 계속 갱신하면서 최단경로를 구하는 알고리즘입니다. 즉, 그리디 알고리즘의 한 유형으로도 볼 수 있습니다. 지금 있는 거보다 더 좋은, 더 짧은 거리가 나왔다면 바로바로 업데이트해 주는 것이죠!
즉, 아이디어는 출발노드에서 가까운 노드부터 차례대로 최단 경로를 찾습니다. 출발 노드에서부터 가장 가깝다고 한 번 결정된 최단 경로는 절대 바뀌지 않고, 출발 노드에서 더 먼 노드의 최단 경로를 구할 때 이용됩니다.
🚗 손으로 이해하기
예시를 통해서 이해해 보겠습니다. 위에서 본 그래프에서 A에서 출발하여 각 노드에 대한 최단 거리를 구해보겠습니다.

0️⃣ 단계

- 먼저, 첫번째 단계는 출발 노드 A에서 시작합니다. A에서 각 노드까지의 최단 거리를 구하고, 리스트에 저장합니다.
- A에서 A까지의 거리는 0이고, A에서 B와 D로의 거리는 각각 2, 3이며, C, E, F, G로는 경로가 없기 때문에 INF(무한대)로 표시합니다.
1️⃣ 단계
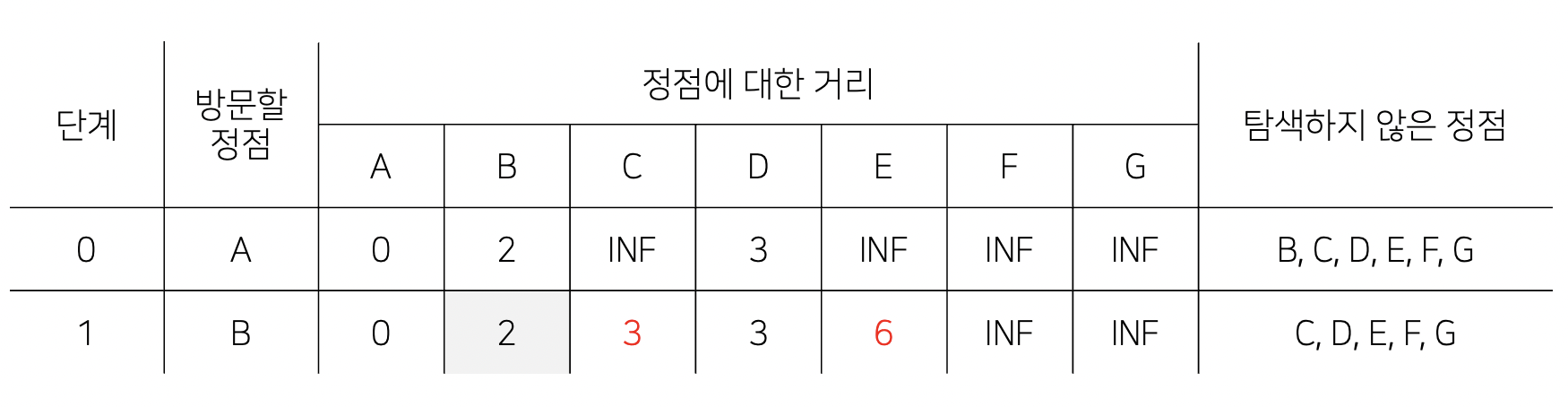
- 그 다음 단계에서 방문할 노드는 A에서 가장 가까운 정점 중에서 아직 탐색하지 않은 정점인 B입니다. (즉, A에서 B로의 최단 경로는 이제 고정입니다)
- B에 방문하여, 탐색하지 않은 모든 정점에 대해서 A에서 B를 거쳐서 각 정점까지의 새로운 거리가 이전 단계에서의 거리와 비교합니다.
- 탐색하지 않은 정점에서 B를 제거합니다. (방문한 노드에 B를 추가합니다.)
- 새로운 거리가 이전 단계에서의 거리보다 짧다면 거리를 저장하는 1차원 리스트의 값을 갱신합니다.
- A → B → C의 최단 경로는 A → B의 최단 거리인 2와 B → C의 거리인 1을 더한 3이 되고, 이 값이 0단계에서 계산한 INF보다 작으므로 A → C의 최단 거리를 3으로 갱신합니다. (2 + 1 < INF)
- A → B → E의 최단 경로는 A → B로의 최단 거리인 2와 B → C의 최단 거리 4을 더한 6이 되고, 이 값이 0단계에서 계산한 INF보다 작으므로 A → C의 최단 거리를 6으로 갱신합니다. (2 + 4 < INF)
- 정점 F와 G는 A에서 B를 거치더라도 갈 수 있는 경로가 없기 때문에 INF값을 유지합니다.
2️⃣단계
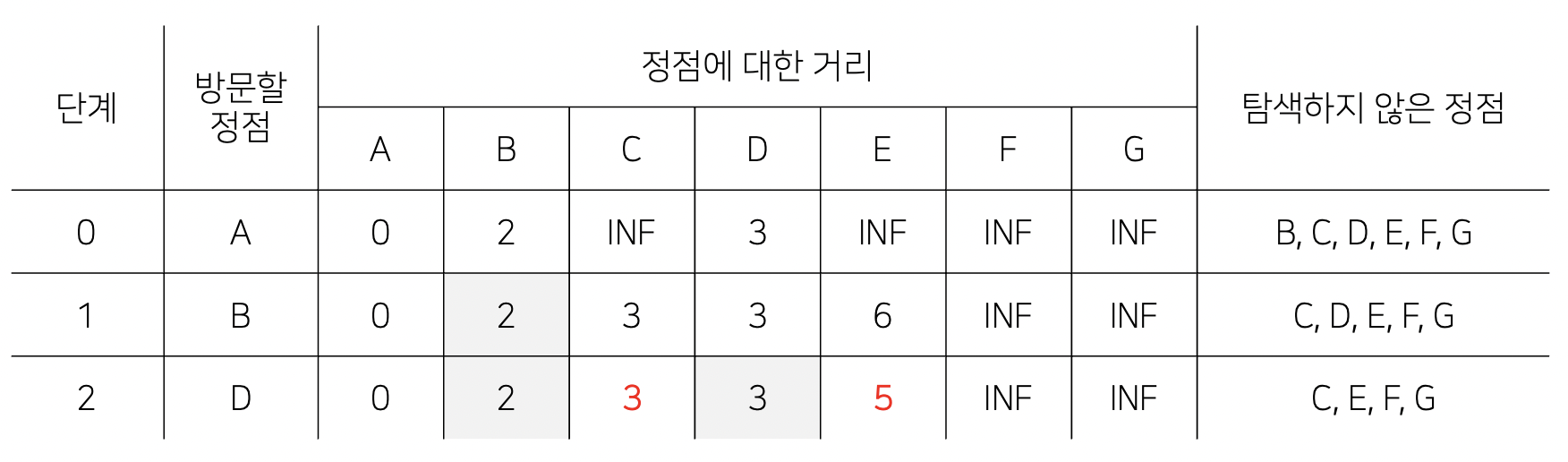
- 1단계 후, 탐색하지 않은 정점들 중에서 가장 가까운 정점은 C, D입니다. 임의로 D를 선택하여 방문하겠습니다. (즉, 이제 A에서 D로의 최단 거리는 3으로 고정입니다.)
- 탐색하지 않은 정점에서 D를 제거합니다. (방문한 노드에 D를 추가합니다.)
- A → D → E의 최단경로는 (A → D의 최단 거리 3) + (D → E의 최단 거리 2) = 5가 되고, 이 값이 이전 단계에서의 최단 거리인 6보다 작으므로 A → E의 최단 거리를 5로 갱신합니다. (3 + 2 < 6)
- A → D → C의 최단 경로는 (A → D의 최단 거리 3) + (D → C의 최단 거리 INF) = INF가 되고, 이 값이 이전 단계에서의 최단 거리인 3보다 크므로 이전 값을 유지합니다. (3 + INF > 3)
- 마찬가지로 정점 F와 G도 D를 거쳐갈 수 있는 경로가 없기 때문에 INF값을 유지합니다.
3️⃣ 단계

- 2단계 후, 탐색하지 않은 정점들 중에서 가장 가까운 정점인 C를 방문합니다.
- 탐색하지 않은 정점에서 C를 제거합니다.
- A → C → F의 최단경로는 (A → C의 최단 거리 3) + (C → F의 최단 거리 5) = 8이 되고, 이 값이 이전 단계에서의 최단 거리인 INF보다 작으므로 A → F의 최단 거리를 8로 갱신합니다. (3 + 5 < INF)
- A → C → E의 최단 경로는 (A → C의 최단 거리 3) + (C → E의 최단 거리 INF) = INF가 되고, 이 값이 이전 단계에서의 최단 거리인 5보다 크므로 이전 값을 유지합니다. (3 + INF > 5)
- A → C → G의 최단 경로는 (A → C의 최단 거리 3) + (C → G의 최단 거리 INF) = INF가 되고, 이 값이 이전 단계에서의 최단 거리인 INF와 같으므로 유지합니다.
4️⃣ 단계

- 3단계 후, 탐색하지 않은 정점들 중에서 가장 가까운 정점인 E를 방문합니다.
- 탐색하지 않은 정점에서 E를 제거합니다.
- A → E → F의 최단경로는 (A → E의 최단 거리 5) + (E → F의 최단 거리 1) = 6이 되고, 이 값이 이전 단계에서의 최단 거리인 8보다 작으므로 A → F의 최단 거리를 6으로 갱신합니다. (5 + 1 < 8)
- A → C → G의 최단 경로는 (A → E의 최단 거리 5) + (E → G의 최단 거리 INF) = INF가 되고, 이 값이 이전 단계에서의 최단 거리인 INF와 같으므로 유지합니다.
5️⃣ 단계

- 4단계 후, 탐색하지 않은 정점들 중에서 A와 가장 가까운 정점인 F를 방문합니다.
- 탐색하지 않은 정점에서 F를 제거합니다.
- A → F → G의 최단 경로는 (A → F의 최단 거리 6) + (F → G의 최단 거리 INF) = INF가 되고, 이 값이 이전 단계에서의 최단 거리인 INF와 같으므로 유지합니다.
이런 식으로 5단계까지 거처셔 A에서 각 노드까지의 최단 거리를 구하였습니다. B로의 최단거리는 2이고, C와 D로의 최단 거리는 3, E로의 최단거리는 5, F로의 최단거리는 6이고, G로의 최단 거리는 존재하지 않습니다.
🚗 코드 구현
위의 단계들을 코드로 구현해보도록 하겠습니다. (<이것이 코딩테스트다>(나동빈, 한빛미디어) 코드를 참고하여 작성하였습니다.)
import sys
input = sys.stdin.readline
INF = int(1e9)
# 노드의 개수, 간선의 개수 입력받기
n, m = map(int, input().split())
# 시작 노드 번호 입력받기
start = int(input())
# 각 노드에 연결되어 있는 오드에 대한 정보를 담는 리스트 만들기
graph = [[] for i in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트 만들기
# (n+1의 크기로 만들어 노드의 번호를 인덱스로 바로 접근할 수 있도록 함)
visited = [False] * (n + 1)
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
# 모든 간선 정보 입력받기
for _ in range(m):
u, v, w = map(int, input().split()) # u: 시작 노드, v: 끝 노드, w: 가중치 (u번 노드에서 b번 노드로 가는 비용이 w)
graph[u].append((v, w))
# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_closest_node():
min_value = INF
index = 0 # 가장 최단 거리가 짧은 노드(index)
for i in range(1, n + 1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
distance[start] = 0 # 시작 노드에 대해서 초기화
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
# 시작 노드를 제외한 전체 n-1개의 노드에 대해 반복
for i in range(n-1):
# 현재 최단 거리가 가장 짧은 노드에 방문
now = get_closest_node()
visited[now] = True
# 현재 노드와 연결된 다른 노드 확인
for j in graph[now]:
cost = distance[now] + j[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[j[0]]:
distance[j[0]] = cost
# 다익스트라 알고리즘 수행
dijkstra()
# 모든 노드로 가기 위한 최단 거리 출력
for i in range(1, n + 1):
# 도달할 수 없는 경우, INF 출력
if distance[i] == INF:
print("INF")
else:
print(distance[i])크게 두 개의 함수로 구현하였습니다.
get_closest_node()
: 방문하지 않은 노드 중에서 가장 가까운 거리에 있는 노드를 선택해주는 함수입니다.dijkstra():get_closest_node()에서 선택한 노드(현재 노드)에 방문하여, 연결된 다른 노드들을 확인합니다. 현재 노드를 거쳐서 다른 노드로 이동하는 거리다 더 짧은 경우, 거리 리스트의 값을 갱신해줍니다.
🚗 시간복잡도
위 코드의 시간복잡도는 $O(V)$입니다.(여기서 $V$는 노드의 개수입니다.) get_smallest_node()함수에서 가장 가까운 노드를 선형 탐색하는 것이 $O(V)$번이고, djikstra() 함수에서 현재 노드에 연결된 다른 노드들을 확인해야 하기 때문입니다.
위의 코드로 백준1753번(최단경로)문제를 제출해보았습니다. 그런데,,

짜잔 시간 초과가 뜹니다😇
시간복잡도를 줄인 코드를 작성해야 할 것 같습니다. 그럼, 개선된 성능의 코드를 구현해보도록 하겠습니다. (<이것이 코딩테스트다>(나동빈, 한빛미디어) 코드를 참고하여 작성하였습니다.)
🚗 개선된 다익스트라 알고리즘 코드
시간복잡도를 줄인 다익스트라 알고리즘에서는 방문할 노드를 선택하는 과정 즉, 방문하지 않은 노드 중에서 가장 가까운 노드를 선택하는 과정(get_closest_node())을 선형탐색이 아닌 힙(Heap) 자료구조를 사용하여 구현합니다.
힙 자료구조를 이용하게 되면 특정 노드까지의 최단 거리에 대한 정보를 힙에 담아서 처리하므로 출발 노드로부터 가장 거리가 짧은 노드를 더욱 빠르게 찾을 수 있습니다. 이전 코드에서는 선형 시간($O(V)$)이 걸렸었는데 힙을 이용하면 로그 시간($O(logV)$)이 걸립니다. (선형에서 로그로 줄어들면 속도가 매우 빨라집니다.)
힙에 대한 자세한 설명은 아래 글을 참고해주세요:)
Data Structure - Heap (힙) | Python 구현
Heap은 이진트리의 변형된 자료구조라고 할 수 있는데, 최댓값 최솟값을 빠르게 찾아야 할 때 많이 사용된다. 📌Heap : 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리 (Com
eunbin00.tistory.com
파이썬의 heapq 라이브러리는 원소로 튜플을 입력받으면 튜플의 첫 번재 원소를 기준으로 우선순위 큐를 구성합니다. 따라서 (거리, 노드 번호)로 튜플 데이터로 구성하여 우선순위 큐에 넣으면 거리순으로 정렬됩니다.
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)
n, e = map(int, input().split())
start = int(input())
graph = [[] for _ in range(n + 1)]
distance = [INF] * (n + 1)
for _ in range(e):
a, b, c = map(int, input().split())
graph[a].append((b, c))
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q: # 큐가 비어있지 않다면
dist, current = heapq.heappop(q)
if distance[current] < dist:
continue # 현재 노드가 이미 처리된 적이 있는 노드라면 무시
for i in graph[current]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
for i in range(1, n + 1):
if distance[i] == INF:
print("INF")
else:
print(distance[i])힙을 사용하는 코드에서는 노드 방문 여부를 확인하는 방법이 다릅니다. 방문 여부를 저장하는 리스트를 사용하지 않고, 우선순위에서 뽑아온 node의 최단거리가 distance에 저장된 값보다 작다면 이미 이전에 갱신되었다는 의미이므로 방문한 적이 있는 노드로 취급합니다.
이전 코드와 비교하면 get_closest_node() 함수를 사용하여 선형 탐색을 하는 것이 아니라, heapq.heappop()을 사용하여 바로 꺼내옵니다. 이 때 걸리는 시간복잡도가 $O(logN)$입니다. 그리고 노드 방문후, 해당 노드에 연결되어 있는 간선들을 차례대로 검사하는 과정은 그대로 선형 시간($O(N)$)이 걸립니다. 따라서 최종 시간복잡도는 $O(NlogN)$이 걸립니다.
위의 코드로 제출을 하면,,

맞았습니다!!🔥
'Algorithm' 카테고리의 다른 글
| Union Find 알고리즘 | 개념과 Python 코드 구현 (0) | 2022.07.01 |
|---|---|
| 다이나믹 프로그래밍(DP, Dynamic Programming) (0) | 2022.06.27 |
| [Algorithm 완전 정복] 다이나믹 프로그래밍 | Dynamic Programming | 계속 쓰일 값은 저장해놓고 가져다 쓰자 (0) | 2021.12.10 |
| [Algorithm 완전 정복] 지금 당장 좋은 것만 고르는 그리디 greedy (0) | 2021.08.22 |
| Recursive Call (재귀함수, 재귀호출) (0) | 2021.05.07 |




댓글